Problem Set 7

part I due by 10 p.m. on Friday, July 25, 2025
part II due by 10 p.m. on Monday, July 28, 2025

Preliminaries

In your work on this assignment, make sure to abide by the policies on academic conduct for this course.

If you have questions while working on this assignment, please come to office hours, post them on Ed Discussion, or email cscis111-staff@lists.fas.harvard.edu

Part I

55 points total

Creating the necessary folder

Create a subfolder called ps7 within your s111 folder, and put all of the files for this assignment in that folder.

Creating the necessary file

The problems from Part I will all be completed in a single PDF file. To create it, you should do the following:

1. Access the template that we have created by clicking on this link and signing into your Google account as needed.

2. When asked, click on the Make a copy button, which will save a copy of the template file to your Google Drive.

3. Select File->Rename, and change the name of the file to ps7_partI.

4. Add your work for the problems from Part I to this file.

5. Once you have completed all of these problems, choose File->Download->PDF document, and save the PDF file on your machine. The resulting PDF file (ps7_partI.pdf) is the one that you will submit. See the submission guidelines at the end of Part I.

Problem 1: Sorting practice

14 points; 2 points for each part; individual-only

Given the following array:

{10, 18, 4, 24, 33, 40, 8, 3, 12}

1. If the array were sorted using selection sort, what would the array look like after the second pass of the algorithm (i.e., after the second time that the algorithm performs a pass or partial pass through the elements of the array)?

2. If the array were sorted using insertion sort, what would the array look like after the fourth iteration of the outer loop of the algorithm?

3. If the array were sorted using Shell sort, what would the array look like after the initial phase of the algorithm, if you assume that it uses an increment of 3? (The method presented in lecture would start with an increment of 7, but you should assume that it uses an increment of 3 instead.)

4. If the array were sorted using bubble sort, what would the array look like after the third pass of the algorithm?

5. If the array were sorted using the version of quicksort presented in lecture, what would the array look like after the initial partitioning phase?

6. If the array were sorted using radix sort, what would the array look like after the initial pass of the algorithm?

7. If the array were sorted using the version of mergesort presented in lecture, what would the array look like after the completion of the fourth call to the merge() method—the method that merges two subarrays? Note: the merge method is the helper method; is not the recursive mSort method.

Problem 2: Counting comparisons

6 points total; 2 points each part; individual-only

Given an already sorted array of 5 elements, how many comparisons of array elements would each of the following algorithms perform?

1. insertion sort

2. bubble sort

3. quicksort

Give an exact number of comparisons for each algorithm, and explain each answer briefly.

Problem 3: Comparing two algorithms

6 points total; 3 points each part; individual-only

Suppose that you want to count the number of duplicates in an unsorted array of n elements. A duplicate is an element that appears multiple times; if a given element appears x times, x - 1 of them are considered duplicates. For example, consider the following array:

{10, 6, 2, 5, 6, 6, 8, 10, 5}

It includes four duplicates: one extra 10, two extra 6s, and one extra 5.

Below are two algorithms for counting duplicates in an array of integers:

Algorithm A:

public static int numDuplicatesA(int[] arr) {
    Sort.mergesort(arr);
    int numDups = 0;
    for (int i = 1; i < arr.length; i++) {
        if (arr[i] == arr[i - 1]) {
            numDups++;
        }
    }
    return numDups;
}

Algorithm B:

public static int numDuplicatesB(int[] arr) {
    int numDups = 0;
    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] == arr[i]) {
                numDups++;
                break;
            }
        }
    }
    return numDups;
}

1. What is the worst-case time efficiency of algorithm A in terms of the length n of the array? Make use of big-O notation and explain your answer briefly.

2. What is the worst-case time efficiency of algorithm B in terms of the length n of the array? Make use of big-O notation and explain your answer briefly.

Problem 4: Sum generator

12 points total; 3 points each part; individual-only

Let’s say that you want to implement a method generateSums(n) that takes an integer n and generates and prints the following series of sums:

1
1 + 2
1 + 2 + 3
...
1 + 2 + ... + n.

For example, generateSums(4) should print the following:

1
3
6
10

One possible implementation of this method is:

public static void generateSums(int n) {
    for (int i = 1; i <= n; i++) {
        int sum = 0;
        for (int j = 1; j <= i; j++) {
            sum = sum + j; // how many times is this executed?
        }
        System.out.println(sum);
    }
}

1. Derive an exact formula for the number of times that the line that increases the sum is executed, as a function of the parameter n.

2. What is the time efficiency of the method shown above as a function of the parameter n? Use big-O notation, and explain your answer briefly.

3. Create an alternative, non-recursive implementation of this method that has a better time efficiency.

4. What is the time efficiency of your alternative implementation as a function of the parameter n? Use big-O notation, and explain your answer briefly.

Problem 5: Practice with references I

12 points total; individual-only

As discussed in lecture, a doubly linked list consists of nodes that include two references: one called next to the next node in the linked list, and one called prev to the previous node in the linked list. The first node in such a list has a prev field whose value is null, and the last node has a next field whose value is null.

The top portion of the diagram below shows a doubly linked list of characters that could be used to represent the string "ran".

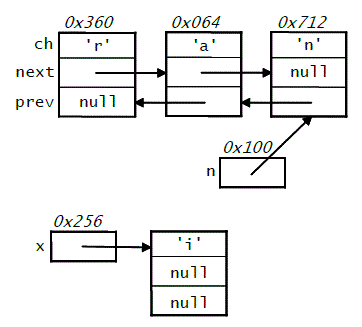
Each of the nodes shown is an instance of the following class:

public class DNode {
    private char ch;
    private DNode next;
    private DNode prev;
}

(In the diagram, we have labeled the individual fields of the DNode object that contains the character 'r'.)

In addition to the list representing "ran", the diagram shows an extra node containing the character 'i', and two reference variables: n, which holds a reference to the third node in the list (the 'n' node); and x, which holds a reference to the 'i' node. The diagram also shows memory addresses of the start of the variables and objects. For example, the 'r' node begins at address 0x360.

Complete the table we have provided in ps7_partI, filling in the address and value of each expression from the left-hand column. You should assume the following:

• the address of the ch field of a DNode is the same as the address of the DNode itself

• the address of the next field of a DNode is 2 more than the address of the DNode itself

• the address of the prev field of a DNode is 6 more than the address of the DNode itself, which means that it is also 4 more than the address of the next field.

Problem 6: Practice with references II

5 points total; individual-only

Given the information provided in Problem 5, write a Java code fragment that inserts the 'i' node between the 'a' node and the 'n' node, producing a linked list that represents the string "rain". Your code fragment should consist of a series of assignment statements. You should not make any method calls, and you should not use any variables other than the ones provided in the diagram. Make sure that the resulting doubly linked list has correct values for the next and prev fields in all nodes.

Testing your code fragment
You should start by convincing yourself on paper that your code is correct. Draw the necessary diagrams and trace through your code, making sure that it works correctly.

Once you have checked your work on paper, you can make use of a simple version of the DNode class that we have created.

To use it, you should click on this link and save the file in your ps7 folder.

Open the ps7 folder in VSCode, and you should see a simple DNode class that includes:

• the definitions of the fields

• a DNode constructor

• a convert method that can be used to convert a Java String object to a doubly-linked list of DNode objects

• a toString() method that allows us to print a DNode object and see the corresponding string

• a main method with some initial test code – including code that sets up the initial diagram that we have provided above.

To test your code fragment, you can add your lines of code to the specified section of the main method and run the program to see if you get the correct result.

The output of the program that we have provided should be:

before changes to list: ran
after changes to list: rain

Submitting your work for Part I

Submit your ps7_partI.pdf file by taking the following steps:

1. If you still need to create a PDF file, open your file on Google Drive, choose File->Download->PDF document, and save the PDF file on your machine.

2. Click on the name of the assignment in the list of assignments on Gradescope. You should see a pop-up window labeled Submit Assignment. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

3. Choose the Submit PDF option, and then click the Select PDF button and find the PDF file that you created. Then click the Upload PDF button.

4. You should see a question outline along with thumbnails of the pages from your uploaded PDF. For each question in the outline:

   • Click the title of the question.
   • Click the page(s) on which your work for that question can be found.

   As you do so, click on the magnifying glass icon for each page and doublecheck that the pages that you see contain the work that you want us to grade.

5. Once you have assigned pages to all of the problems in the question outline, click the Submit button in the lower-right corner of the window. You should see a box saying that your submission was successful.

Part II

45-55 points total

Problem 7: Searching an array for pairs that sum to a specified value

20-30 points total; pair-optional

Getting started

1. If you haven’t already done so, create a folder named ps7 for your work on this assignment. You can find instructions for doing so here.

2. Download our Sort class from lecture, making sure to save it in your ps7 folder:

   • Sort.java, our Sort class from lecture

3. In VS Code, select the File->Open Folder or File->Open menu option, and use the resulting dialog box to find and open your ps7 folder. (Note: You must open the folder; it is not sufficient to simply open the file.)

4. Select File->New File, which will open up an empty editor window.

5. Select File->Save, and give the new file the name Problem7.java.

6. In the new file, create a class called Problem7.

Overview

Suppose you are given an array of n integers, and you need to find all pairs of values in the array (if any) that sum to a given integer k. In a class named Problem7, write code that performs this task for you and outputs all of the pairs that it finds. For example, if k is 12 and the array is {10, 4, 7, 7, 8, 5, 15}, your code should output something like the following:

4 + 8 = 12
7 + 5 = 12
7 + 5 = 12

Note that we get two 7 + 5 sums because 7 appears twice in the array. However, while the method or methods that you write may print a given pair of values more than once in such cases, it is not necessary to do so. In addition, the order in which the sums (and the terms within each sum) are printed does not matter.

Your tasks

1. (20 points) In your Problem7 class, implement a static method named pairSums() that requires O(n²) steps to solve this problem. The method should have the following header:

   public static void pairSums(int k, int[] arr)
   

   If arr is null, the method should throw an IllegalArgumentException.

   Other requirements:

   • In the comments that accompany the method, include a brief argument showing that your algorithm has a time efficiency of O(n*²).*

   • Your method must use O(1) extra memory – i.e., only a fixed number of local variables. It should not use a separate array.

   • Include a main method with code that tests your new method. Recall that that you can use the Arrays.toString() method to convert an array to a string; import the java.util. package to gain access to the Arrays class. You should include at least two separate test cases.

2. (10 points; required of grad-credit students; “partial” extra credit for others) Implement a static method named pairSumsImproved() that takes the same parameters as pairSums, but that requires only O(nlogn) steps in the average case to solve this problem.

   Hint: You should begin by sorting the array using one of the methods from our Sort class, which your downloaded above.

   Other requirements:

   • Once the array has been sorted, your method must perform only O(n) additional steps to find and print the pairs. In addition, the overall time efficiency (i.e., of the sorting algorithm followed by your additional steps) should be O(nlogn) in the average case.

   • The comments above the method should include a brief argument showing that your algorithm has a time efficiency of O(nlogn) in the average case.

   • The steps that your method takes after sorting the array must use O(1) extra memory. The sorting algorithm that you call can use more memory, but the rest of your method should use O(1) memory – i.e., only a fixed number of local variables.

   • You method should again throw an exception if arr is null.

   • Add at least two test cases for your new method to the main method.

Problem 8: Finding the union of two arrays

25 points; individual-only

Getting started

1. As needed, select the File->Open Folder or File->Open menu option, and use the resulting dialog box to find and open your ps7 folder. (Note: You must open the folder; it is not sufficient to simply open the file.)

2. Select File->New File, which will open up an empty editor window.

3. Select File->Save, and give the new file the name Problem8.java.

4. In the new file, create a class called Problem8.

Your task

In your Problem8 class, implement a method with the following header

public static int[] union(int[] a1, int[] a2)

It should take two arrays of integers a1 and a2, and it should use an approach based on merging to create and return a new array containing the union of the values in a1 and a2 – i.e., all values that are found in one or both of the original arrays. The result should be in sorted order, and it should not include any duplicate values. For example, if you add the following test code to a main method in Problem8:

int[] a1 = {10, 5, 7, 5, 9, 4};
int[] a2 = {7, 5, 15, 7, 7, 9, 10};
int[] result1 = union(a1, a2);
System.out.println("result1: " + Arrays.toString(result1));

int[] a3 = {0, 2, -4, 6, 10, 8};
int[] a4 = {12, 0, -4, 8};
int[] result2 = union(a3, a4);
System.out.println("result2: " + Arrays.toString(result2));

it should display:

result1: [4, 5, 7, 9, 10, 15, 0, 0, 0, 0, 0, 0, 0]
result2: [-4, 0, 2, 6, 8, 10, 12, 0, 0, 0]

(Note that we end up with extra 0s at the end of both of these result arrays for reasons that are discussed below.)

For full credit, your method must be as efficient as possible. See below for more details.

Required approach

1. Begin by creating a new array for the union, giving it a length that is the sum of the lengths of the two original arrays.

2. Use one of the more efficient sorting algorithms from our Sort class to sort both of the original arrays. If you have downloaded our Sort class into the same folder as your Problem8 class (see the Getting started section at the start of Problem 7), you should be able to make method calls to an appropriate method in the Sort class from within your union method.

3. Find the union of the two arrays by employing an approach that is similar to the one that we used to merge two sorted subarrays (i.e., the approach taken by the merge method in Sort.java)—using indices to “walk down” the two original arrays and copy their values into the array that you created for the union.

   Important notes:

   • One important difference between merging and finding the union is that the union should not include any duplicates. In other words, a given number that appears in one or both of the original arrays should appear exactly once in the union. As a result, you will need to include code that skips over duplicate values as needed as you walk down the original arrays.

   • Your algorithm should be as efficient as possible. In particular, you should perform at most one complete pass through each of the arrays.

4. At the end of the method, return a reference to the array containing the union.

5. Add test code for your method to a main method. Recall that that you can use the Arrays.toString() method to convert an array to a string; import the java.util. package to gain access to the Arrays class. In addition to the cases shown above, you should include at least one other test case that you create.

Notes:

• Because we don’t include duplicates in the result, the number of values in the union (call it x) can be smaller than the length of the results array (which should be the sum of the lengths of the original arrays). In such cases, you should end up with extra 0s at the end of the results array as shown in both of our test cases above.

  If 0 appears in one or both of the original arrays, it will also show up earlier in the results array as part of the union, as it does in our second example above.

• If either a1 or a2 is null, the method should throw an IllegalArgumentException.

Submitting your work for Part II

You should submit only the following files:

• Problem7.java
• Problem8.java

You do not need to submit Sort.java.

Here are the steps:

1. Click on the name of the assignment in the list of assignments. You should see a pop-up window with a box labeled DRAG & DROP. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

2. Add your files to the box labeled DRAG & DROP. You can either drag and drop the files from their folder into the box, or you can click on the box itself and browse for the files.

3. Click the Upload button.

4. You should see a box saying that your submission was successful. Click the (x) button to close that box.

5. The Autograder will perform some tests on your file. Once it is done, check the results to ensure that the tests were passed. If one or more of the tests did not pass, the name of that test will be in red, and there should be a message describing the failure. Based on those messages, make any necessary changes. Feel free to ask a staff member for help.

   Note: You will not see a complete Autograder score when you submit. That is because additional tests will be run later, after the final deadline for the submission has passed. For such problems, it is important to realize that passing all of the initial tests does not necessarily mean that you will ultimately get full credit on the problem. You should always run your own tests to convince yourself that the logic of your solutions is correct.

6. If needed, use the Resubmit button at the bottom of the page to resubmit your work. Important: Every time that you make a submission, you should submit all of the files for that Gradescope assignment, even if some of them have not changed since your last submission.

7. Near the top of the page, click on the box labeled Code. Then click on the name of each file to view its contents. Check to make sure that you see the code that you want us to grade.

Last updated on July 24, 2025.